たし算素過程55題と45題を3段階に分ける

素過程程55題と45題をそれぞれ3段階に分けるのはなぜ？という声もありますが、理由は別になくて単に

かんたん
ふつう
むずかしい

がわかりやすくていいかな、と。

教育者向けの専門的な書籍を見ると、たし算素過程55題の5.2進法は6種類に型分けできる…なんて書いてあるのですが、学習する側にしても、6段の階段を登るよりは3段のほうが見通しがきいてやる気が失せずにすむのではと思いました。

自分がやる側になったら「これ6種類あるからね」と言われるより、「これ3段階になってるから」と言われたほうがチャレンジしてみようか、という気になりますから。

さて、くりあがりなし55題の分け方ですが、5.2進法では5がひとつの単位ですから、

かんたん問題は
5までのたし算

ふつう問題は
6＋2のように、5のかたまりはすでにあり、残りの数に足す数をプラスするたし算

むずかしい問題は
3＋4のように、足す数を分解して5のかたまりを作り、残りの数をプラスするたし算

と分けることにしました。

0を含むたし算はどうすればよいか

ここまではなんとか分けることができたのですが、悩んだのが0の扱い。

0を含むたし算は、0という概念の理解が難しいため、教育現場ではあらためてその部分だけ別に学習するようですが、そうなると0＋□、□+0だけで問題を作ることになります。

いくら0の概念が難しいといっても、一枚のプリントの問題すべてが0とのたし算というのでは、簡単すぎやしないだろうか？

そう感じたので、これらの問題も5までと6以上にわけて、5まではかんたん問題、6以上はふつう問題に混ぜてしまうことにしました。

次にくりあがりありの45題です。

こちらはなんと専門的には7つの型に分けられるそうです。

ですが強引に3段階、しかもプリント数の都合上、同じくらいの問題数に分けます。

こちらは5.2進法の考え方で

1． 6＋6のように、5のかたまりを2くっつけて、残りをたすたし算

2． 2＋8のように、5のかたまりを2つつくるたし算　和が10

3．6＋9のように、5のかたまりを3つつくるたし算　和が15

4． 4＋7のように、足す数あるいは足される数を5のかたまりにするたし算

5．7＋9のように、5のかたまりを2つくっつけ、残りの数でさらに5のかたまりをつくるたし算

の5つに分けました。

この5つを、かんたん、ふつう、むずかしいの3段階にしようと考えたのですが、単純に1をかんたん問題、2と3をふつう問題、4と5をむずかしい問題にすると、ふつう問題の答えが10と15にしかなりません。

0とのたし算と同じように、これでは簡単すぎるのでは？と思い、2と5でむずかしい問題、3と4でふつう問題とすることにしました。

まとめるとこのようになります。

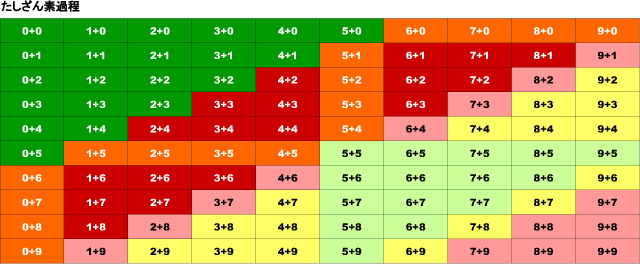
くりあがりなしは白文字の枠です。

緑に白文字がかんたん問題
オレンジに白文字がふつう問題
赤に白文字がむずかしい問題

くりあがりありは黒文字の枠です。

うぐいす色に黒字がかんたん問題
黄色に黒字がふつう問題
桃色に黒字がむずかしい問題

になります。

そして完成した教材はこちら。

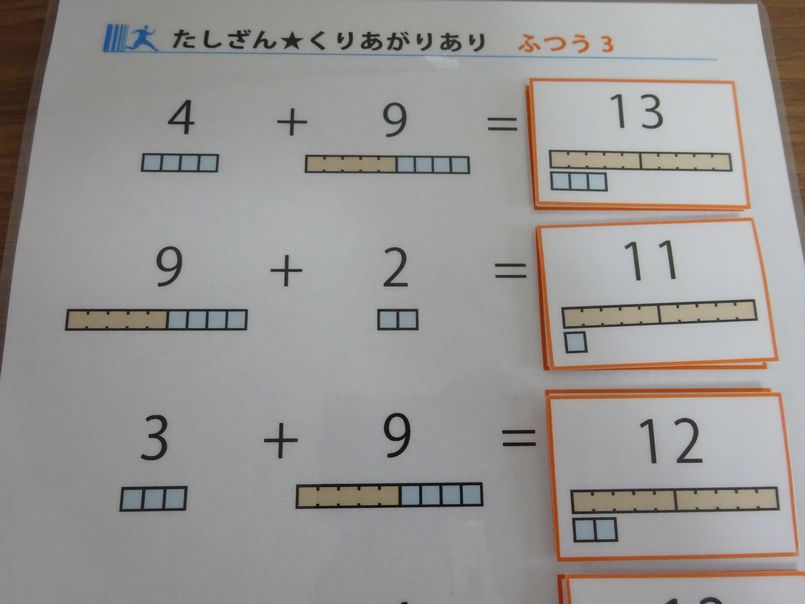
数字の下のマス目はヒントです。

5.2進法なので、5をひとつのかたまりにしています。

しかし、分解することもあるため、目盛りを入れて、5個分ということがわかるようにしました。

10は5のかたまり2つです。

面ファスナーは多少位置がずれてもくっつくように、台紙側は大きめにしていますが、答えの側はそれよりも小さくして、はがすときにあまり力を入れなくてもいいようにしてあります。

この教材はあらかじめ用意されている答えを貼り付けるだけなので、プリント教材よりも簡単です。

さらに、はったりはがしたりの操作が子どもには面白いので、次々に一人で進めようとするかもしれませんが、やはり最初はタイルなどの具体物も使いながら、一緒に学習していくことが大切と思います。

5の合成分解が頭の中でできるようになったら、数字の下のマス目を補助的に使いながら問題を解き進めていけるでしょう。