たし算 素過程の100題をマスターする

たし算の問題作りなんて簡単、と最初は考えていましたが、いざとりかかってみると、10までのくりあがりのないたし算だけでも、すべてを網羅しようとするとかなりの数になることに気がつきました。

これは本腰を入れて作らねばと調べたところ、素過程という基礎計算があることがわかりました。

素過程とは、すべての計算のおおもとになるの1ケタ同士の計算のことで、0から9まで、加減乗除とも100題ずつあります。

たし算なら、0+0から9+9までの100題です。

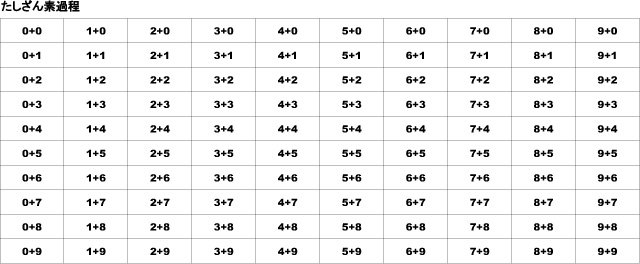
これが素過程の一覧表です。

基礎ですから、これはなんとしてもマスターさせたいところ。

でもいきなり100題全部は無理です。

やはりかんたんなものから難しいものへと段階的にすすめないと。

ということで、100題を難易度で分けることにしました。

5.2進法で素過程を難易度別にわける

100題をどう分けるか、で誰でも思いつくのが、くりあがりのあるものとないもの。

全部混ぜて暗記してしまえばいいという意見もありますが、それができない子もいます。

小さい数から少しずつ理解を進めるやり方が王道と思います。

100題のうち、くりあがりのない足し算は55題、くりあがりのある足し算は45題です。

いっぺんに覚えるにはまだ多い。

そこで、さらにこの55題と45題を難易度で分けます。

このときに参考にしたのが5.2進法です。

5.2進法とは、5をひとつの単位（かたまり）として、たとえば6は5と1、10は5が2つ、というように考えます。

10の数をイメージするのは大変でも、5までの数がイメージできれば、あとはその合成分解で計算を進められるので理解しやすいと言われます。

5.2進法については、小学校の先生のための算数授業公開チャンネルを開設している石原清貴氏の動画「算数授業（タイルと5.2進法について）」が理解を助けてくれます。

5.2進法を取り入れながら、かつ問題が単調にならないように難易度別に分けてみました。